[P.S.: My apologies to readers who may be averse to numbers, as this post leans more toward the analytical side of the spectrum.]
This week, an article in the Financial Times caught my attention. In essence, the piece highlights the growing trend of highly educated young Chinese individuals with increasing career aspirations. However, the Chinese economy struggles to provide an adequate number of high-skilled jobs, leading to dissatisfaction among the graduate community. Conversely, the Chinese government observes that numerous low-skilled positions are failing to draw sufficient talent, placing certain industries at risk. As I delved into the article, it evoked memories of my student years and brought to mind a classic ‘game theory’ dilemma that I would like to elucidate here.
First, let us define game theory. According to the Britannica dictionary, ‘game theory’ refers to a “branch of applied mathematics that offers tools for examining situations where parties, known as players, make interdependent decisions. This interdependence prompts each player to take into account the other player’s potential decisions, or strategies, when formulating their own strategy.” While certain aspects of game theory can be traced back to the 15th and 16th centuries, the field truly gained momentum in the early 20th century under the influence of distinguished mathematicians such as John von Neumann and John Nash (whose life is portrayed in the film ‘A Beautiful Mind‘). Game theory has expanded beyond the realm of mathematics; for example, antitrust authorities occasionally employ this framework to simulate potential competition scenarios (maybe as part of the controversial Microsoft – Activision deal, who knows?).
Back to China. Let us say, to simplify, that the country has only 2 young people, who each need to decide whether they pursue studies or not. In one hand, studies give them access to better-paying and qualified roles. On the other hand, studying costs (in time, effort and money) and the promising pay will diminish as competition for the same type of qualified jobs increases. The State, on its side, wants to maximize the total value created by those two people. Which path should each student follow? And will the students’ individual preferences coincide with the State’s preference?
Game theory helps us solve this problem in an ‘analytical’ way. What we need is to make some assumptions on the ‘payoff’ (representing a blended mix of pay, satisfaction etc.) that each student will receive depending on the scenario will end up in:
- For instance, if a person decides to study but the other does not, the ‘studying person’ receives 5 points, the ‘non-studying’ receives 2 (lower pay but no need to go to university);
- If both decide to study, they compete against each other for the qualified jobs, resulting in lower salary and thus satisfaction. We thus assume each gets 3 points;
- Finally, if none decides to study, there is also competition, but for the unqualified and lower-paying role, they both get only 1 point.
In ‘prescriptive form’, we can summarise the various possibilities as follows:
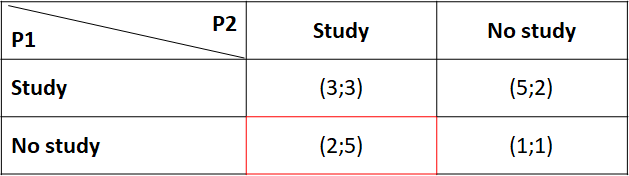
For instance, the red box should read as ‘If the first player (P1) decides not to study while the second (P2) decides to, the first player receives 2 points (first value between brackets) whereas the second receives 5 (second value)’. We can here verify that the game is symmetrical – Players could exchange seats without changes to payout.
Now we are in the shoes of Player 1. What would be his best decision if he knew what Player 2 does? Well:
- If P2 decides to study, P1 has the choice to study too (payout of 3) or not to study (payout of 2). 3 is greater than 2, so P1 goes for the study option too;
- If P2 decides not to study, P1 gets 5 if he studies, 1 if he does not. Similarly, P1 studies.
What we conclude is thus that P1 should always study, irrespective of what P2 does. We call this a ‘Dominant Strategy’. Same reasoning is also valid for P2. So we end up in an ‘equilibrium’ where both players decide to study and each gets 3. No one has an incentive to deviate and not to study: not studying would mean decreasing the payout from 3 to 2. An equilibrium where no player has an incentive to deviate is called a ‘Nash equilibrium’ – yes, the same Nash as above. Funnily enough (and because I have carefully chosen the figures too!), this equilibrium ‘everyone studies’ is the one depicted in the article.
Is the State happy in that scenario? We said that the State’s payout is assumed to be equal to the sum of the two individual payouts. Here we have 3+3=6. But a careful examination of the table above shows that a case where one decides to study and the other does not is more beneficial to the State, who would get 5+2=7. This suboptimal situation for the State is also described in the article.
If the State increased the tuition fees, for instance, it would mechanically lower the payout in case of studies. It could use part of the money to subsidize salaries for unqualified roles. The table could then become:
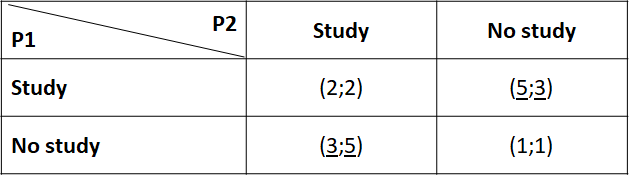
In this situation, by studying each possibility sequentially (as per above), the reader will identify two potential equilibriums, both with one person studying and the other not (underlined in this second table). Both are Nash equilibriums (one you arrive in this situation, no one has an incentive to change his decision). The State is happy, this new total payout of 5+3=8, greater than any other payout in this second table. As a consequence, we could suggest increasing the cost of studying to subsidise the benefit of working in low-qualified jobs as a potential solution to the issue. Cost and benefits can be monetary but also non-monetary, e.g. more selective university entrance exams, renovated cheap housing near factories.
While the outcome in this specific case is fairly predictable and might have been anticipated without any mathematical analysis, I hope this post has provided you with a clearer understanding of the diverse scenarios that more advanced analytical techniques can help illuminate.
